Rotation du plan d'oscillation et projection du vecteur rotation instantanée.

Représentons la rotation de la Terre , par rapport aux "axes de la mécanique" (référentiel galiléen), par un vecteur noté ,parallèle à l'axe de rotation de la Terre, et orienté du Sud vers le Nord terrestres , et de grandeur :

= 2. / Te

avec Te= 23 h 56 min (jour sidéral) et = 3,14159...

Il est clair qu'un pendule situé au pôle Nord , oscillerait dans le plan de figure , et la Terre tournant , un observateur terrestre verrait le plan d'oscillation du pendule effectuer une rotation par rapport à lui en 24 h.

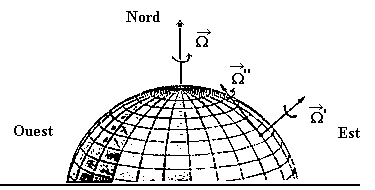
A Nantes, par exemple, ce vecteur rotation se décompose en ' sur la verticale locale et " sur l'horizontale locale. La force de Coriolis , perpendiculaire à chaque instant à et au vecteur vitesse V du centre d'inertie de la boule du pendule, aura aussi deux composantes :

Celle due à " sera verticale (car V est sensiblement horizontal) , et d'effet indétectable (force négligeable par rapport au poids)

Celle due à ' sera horizontale , et étant perpendiculaire à V, produira la rotation du plan des oscillations dans le référentiel terrestre.

Le même raisonnement que ci- dessus , conduit l'observateur terrestre à interpréter la rotation du plan d'oscillation du pendule comme une rotation de vitesse angulaire '.

Or ' = .sin () ; désignant la latitude du lieu (c'est à dire l'angle d'inclinaison du vecteur ' par rapport au plan équatorial terrestre). La période de rotation du plan d'oscillation du pendule sera :

T=To/sin()

Retour à la page d'accueil