Un autre oscillateur paramétrique.(Le Botafumeiro de Saint Jacques de Compostelle) |
Un oscillateur paramétrique est un oscillateur dont un des paramètres descriptifs voit sa valeur varier au cours du temps. Les oscillateurs paramétriques jouent un rôle important en physique (en radioélectricité par exemple).
Un pendule simple peut-être transformé en oscillateur paramétrique : c'est le cas du célèbre " Botafumeiro " de St Jacques de Compostelle : (lire dans un manuel de physique de Terminale) la description de ce dispositif.
Le paramètre qui varie est la longueur du pendule , (ce paramètre est fixe dans le pendule simple ordinaire) , on remarquera que l'élongation angulaire n'est pas un paramètre descriptif, mais la grandeur oscillante. (Ne pas confondre les deux notions).
Ce problème est une analyse de son fonctionnement.
Partie A :
| Dans cette partie, on étudie un pendule simple de masse m ,
de longueur fixe l , suspendu à un point fixe O. L'amplitude
des oscillations est ßm , valeur constante car on néglige
tous les frottements. ß est l'élongation angulaire mesurée à partir de la position d 'équilibre. 1) Calculer la valeur de la tension T1 du fil pour ß = ßm Cette valeur dépend-elle de la longueur l du pendule ? Justifiez. 2) Calculer la valeur de la tension T2 du fil pour ß = 0 Cette valeur dépend-elle de la longueur l du pendule ? Justifiez. 3) Comparez T1 et T2 (en grandeur). |  |
Partie B : On pourra utiliser des résultats de la partie A.
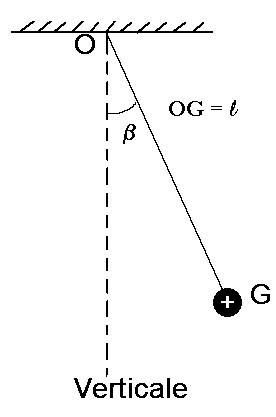
| Un pendule simple est constitué par une masse
m accrochée à un fil de masse négligeable, qui
peut coulisser sans frottement dans une glissière
fixe. Un opérateur tient l'extrémité du fil et peut
modifier la longueur de celui-ci en modifiant sa
traction F sur le fil. L'opérateur raccourcit le fil de dl lorsque le pendule passe par sa position d'équilibre et le laisse s'allonger de dl lorsque ß = ßm :
1) Calculer le travail W1 fourni par l'opérateur lors d'un déplacement BC (ou B'C'). 2) L'ensemble formé par l'opérateur et le pendule est isolé : son énergie est donc constante. En déduire la variation d 'énergie mécanique dE1 du pendule. |  |
| 3) Calculer le travail W2 fourni par l'opérateur lors d'un déplacement DA' (ou D'A). 4) L'ensemble formé par l'opérateur et le pendule est isolé : son énergie est donc constante. En déduire la variation d 'énergie mécanique dE2 du pendule. 5) Calculez la variation dE d 'énergie du pendule pour une oscillation complète de celui-ci 6) Discussion des résultats :
| |
Le centre d'inertie G du pendule décrit
la courbe A, B, C, D, A', B', C', D' de la
figure ,